Грамзиви алгоритми
Алгоритми засновани на претрази до решења долазе кроз низ корака где у сваком кораку анализирају неколико могућности. Алгоритми код којих се уместо анализе различитих могућности у сваком кораку узима неко локално оптимално решење називају се похлепни или грамзиви алгоритми (енгл. greedy algorithms). Такве алгоритме обично има смисла примењивати само код проблема код којих постоји гаранција да ће такви избори на крају довести до глобално оптималног решења.
На слици су приказана два дрвета претраге таква да у случају првог дрвета похлепни алгоритам који у сваком кораку бира наследника са највећом могућом вредношћу доводи до оптималног решења (максималне могуће вредности), док у случају другог дрвета похлепни алгоритам доводи до неоптималног решења (вредности која није оптимална).
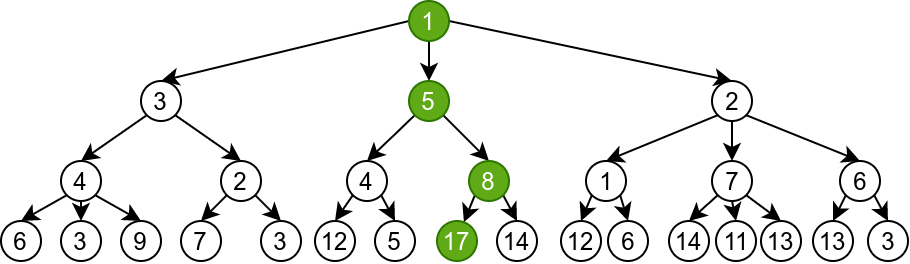
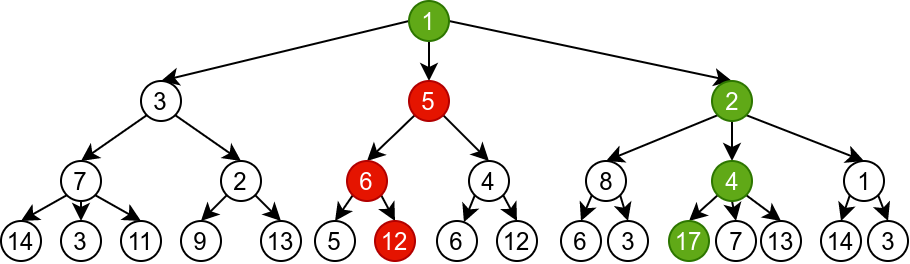
Похлепни алгоритми нам, дакле, пружају јасну стратегију (бирај што бољу од свих расположивих могућности) како да у сваком кораку изаберемо једну од више понуђених могућности тако да на крају дођемо до жељеног оптималног решења. У наставку ћемо појам грамзивих алгоритама мало проширити и разматраћемо алгоритме који у сваком кораку бирају само једну могућност на основу неке прецизно дефинисане стратегије, тако да ти избори гарантују да ће се на крају доћи до жељеног (исправног тј. оптималног) решења проблема.
Похлепни алгоритми не врше испитивање различитих случајева нити исцрпну претрагу и стога су по правилу веома ефикасни (у сваком кораку је извршено максимално могуће одсецање). Такође, обично се веома једноставно имплементирају. Са друге стране, као и код свих других алгоритама у којима се користи одсецање, потребно је унапред доказати да се похлепним алгоритмом добија коректно тј. оптимално решење, што у неким случајевима може бити веома изазовно. Само налажење исправног похлепног алгоритма (тј. стратегије) може представљати озбиљан изазов и често није тривијално одредити да ли за неки проблем постоји или не постоји похлепно решење.
Код неких проблема похлепни алгоритми не доводе увек до оптималног решења, али се може доказати да ће решења која се добијају бити квалитетна и неће се пуно разликовати од оптималних, што може оправдати употребу похлепних алгоритама (јер они могу бити много ефикаснији од исцрпних алгоритама који гарантују оптималност). У том случају похлепни алгоритми су хеуристике (технике које не гарантују да ће увек довести до оптималног решења, али који доводе до довољно добрих решења).
Алгоритми засновани на претрази или на динамичком програмирању обично у сваком кораку разматрају више могућности (којима се добија више потпроблема) и након разматрања свих могућности бирају ону најбољу. Дакле, избор се врши тек након решавања потпроблема. За разлику од тога грамзиви алгоритми унапред знају која могућност ће водити до оптималног решења и избор врше одмах, након чега решавају само један потпроблем. У случају оптмизационих проблема и у случају грамзивих алгоритма потребно је да важи својство оптималне подструктуре тј. да се оптимално решење полазног проблема добија помоћу оптималног решења потпроблема.
Да би се доказала коректност похлепног алгоритма, обично је потребно доказати неколико ствари. Иако ћемо некада грамзивим алгоритмима решавати проблеме у којима се захтева да се испита да се провери да ли постоји неко решење које задовољава дате услове и да се пронађе било које такво решење, најчешће ћемо разматрати проблеме у којима се захтева да се у групи решења која задовољавају неке дате услове (исправних решења) пронађе оно оптимално (у случају када постоји више таквих оптималних решења обично је довољно да се пронађе било које).
Прво је потребно доказати да похлепна стратегија даје решење које је исправно тј. решење које задовољава све услове задатка.
Након тога је потребно доказати и да је решење добијено похлепном стратегијом оптимално. Ти докази су по правилу тежи и постоји неколико техника како се они изводе. Обично се крене од неког решења за које претпостављамо да је оптимално и које не мора бити идентично ономе које смо добили похлепном стратегијом. Оно не може бити горе од решења нађеног на основу похлепне стратегије (јер она враћа једно коректно решење, па оптимум може бити само евентуално бољи од тог решења), а потребно је доказати да не може бити боље.
Једна техника да се оптималност докаже је то да се покаже да се оптимално решење мало по мало, применом трансформације појединачних корака може претворити у решење добијено на основу наше стратегије. Обично је довољно доказати да се први корак оптималног решења може заменити првим кораком који грамзива стратегија сугерише, тако да се коректност и квалитет решења тиме не нарушавају и коректност даље следи на основу индуктивног аргумента. Ову технику називаћемо техника размене (енгл. exchange).
Једна техника да се оптималност докаже је то да се докаже да је решење добијено на основу похлепне стратегије увек по неком критеријуму испред претпостављеног оптималног решења. Ову технику називаћемо похлепно решење је увек испред (енгл. greedy stays ahead).
Једна техника да се оптималност докаже је да се одреди теоријска граница вредности оптимума и да се онда докаже да похлепни алгоритам даје решење чија је вредност управо једнака оптимуму. Ову технику називаћемо техника границе (енгл. structural bound).
